Сравнение дробей 2.04 ? 2.005 Ответ: 2,04 > 2,005
Онлайн калькулятор сравнения дробей позволяет сравнить две дроби и дать ответ какая из них больше (меньше) или они равны.
Дроби могуть быть введены как обыкновенном виде так и в смешанном (с целой частью). Поддерживается ввод отрицательных дробей, для этого введите знак минус "-" в целой части дроби. Можно сравнить дробь с дробью или дробь с целым числом.
Чтобы сравнить дроби введите их числители и знаменатели (или целое число) в соответствующие поля и нажмите кнопку "Сравнить дроби". В резльтате появиться ответ с пошаговым решением и детальное объяснение решения.
Дроби могуть быть введены как обыкновенном виде так и в смешанном (с целой частью). Поддерживается ввод отрицательных дробей, для этого введите знак минус "-" в целой части дроби. Можно сравнить дробь с дробью или дробь с целым числом.
Чтобы сравнить дроби введите их числители и знаменатели (или целое число) в соответствующие поля и нажмите кнопку "Сравнить дроби". В резльтате появиться ответ с пошаговым решением и детальное объяснение решения.
Решение:
Введено
2
04
100
?
2
005
1000
2. Сокращение
2
1 · 4
25 · 4
?
2
1 · 5
200 · 5
2
1
25
?
2
1
200
3. Перевод в обыкновенные
2·25 + 1
25
?
2·200 + 1
200
51
25
?
401
200
4. Под общий знаменатель 200
51 · 8
25 · 8
?
401
200
408
200
?
401
200
Ответ
408 > 401
Детальное объяснение решения:
1.Запишем десятичное число в виде смешанной дроби.
2.04
2
04
100
2.005
2
005
1000
2.Сократим первую дробь на 4. Сократим вторую дробь на 5.
2
04
100
?
2
005
1000
2
1 · 4
25 · 4
?
2
1 · 5
200 · 5
2
1
25
?
2
1
200
3.Перевод смешаных дробей в обыкновенные
2
1
25
?
2
1
200
2·25 + 1
25
?
2·200 + 1
200
51
25
?
401
200
4.Приведение к общему знаменателю 200
Домножитель первой дроби 8
51
25
?
401
200
51 · 8
25 · 8
?
401
200
408
200
?
401
200
408 > 401
Сохраните ссылку на это решение:
Скопировано
Калькулятор сравнения дробей работает по общим правилам вычисления дробей.
Сравнение дробей с одинаковыми знаменателями:
Чтобы сравнить обыкновенные дроби с одинаковыми знаменателями достаточно сравнить числители этих дробей.
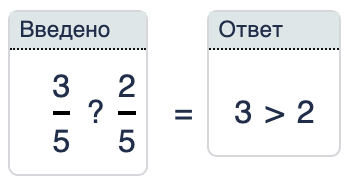
Сравнение дробей с различными знаменателями:
Если знаменатели дробей не равны, то необходимо привести дроби к одному общему знаменателю. После этого получим две другие дроби с одинаковыми знаменателями, которые легко сравнить по их числителям.

Сравнение смешанных дробей или неправильных дробей:
Все смешанные дроби необходимо перевести в неправильные дроби, затем привести к одному общему знаменателю. Далее сравнение дробей осуществляется сравнением их числителей.

Сравнение дробей с одинаковыми знаменателями:
Чтобы сравнить обыкновенные дроби с одинаковыми знаменателями достаточно сравнить числители этих дробей.

Сравнение дробей с различными знаменателями:
Если знаменатели дробей не равны, то необходимо привести дроби к одному общему знаменателю. После этого получим две другие дроби с одинаковыми знаменателями, которые легко сравнить по их числителям.

Сравнение смешанных дробей или неправильных дробей:
Все смешанные дроби необходимо перевести в неправильные дроби, затем привести к одному общему знаменателю. Далее сравнение дробей осуществляется сравнением их числителей.

Похожие калькуляторы:
